Ćwiczenie nr 3

Mikrofalowy czujnik poziomu cieczy

 

1. Zasada działania czujnika.

2. Zasada pomiaru poziomu cieczy za pomocą mikrofalowego rezonatora cylindrycznego.

3. Zasada pomiaru poziomu cieczy przy użyciu ćwierćfalowego rezonatora współosiowego.

3.1. Zdolność rozdzielcza i dokładność czujnika.
3.2. Elektroniczny pomiar częstotliwości rezonansowej czujnika.

4. Zadania do wykonania.

5. Literatura


 

1.  Zasada działania

Podstawą rozważanych metod pomiaru cieczy będą radiotechniczne czujniki położenia. Radiotechniczny czujnik położenia stanowi rezonansowy obwód RLC, zbudowany ze stałych skupionych lub rozłożonych, w którym pojemność elektryczna C=C(x) lub indukcyjność L=L(x) lub obydwie te wielkości są zależne od położenia x. Pomiaru położenia x dokonuje się poprzez pomiar częstotliwości rezonansowej czujnika  fr= fr(x) zależnej od x, przy użyciu przetwornika realizującego funkcję odwrotną x= g(fr) charakterystyczną dla danego typu przetwornika.

Zaletą przetworników radiotechnicznych jest ich duża zdolność rozdzielcza, prosta konstrukcja mechaniczna i wynikająca stąd duża długoczasowa dokładność.

Pomiar częstotliwości rezonansowej przetwornika, a stąd i przemieszczenia, może być prowadzony zdalnie, przy użyciu linii długiej (przewodu współosiowego o małej impedancji falowej). Pozwala to na pomiar przemieszczeń w warunkach, w których nie mogą poprawnie pracować aktywne elementy elektroniczne (np. z powodu wysokiej temperatury lub dużych całkowitych dawek promieniowania jonizującego).

Poniżej rozważane są dwa rodzaje czujników. Pierwszy stanowi mikrofalowy rezonator cylindryczny przestrajany ruchomym tłokiem pływającym na powierzchni cieczy. Drugi rodzaj czujnika stanowi współosiowy rezonator ćwierćfalowy przestrajany zmianą poziomu  wypełniającej go cieczy dielektrycznej.

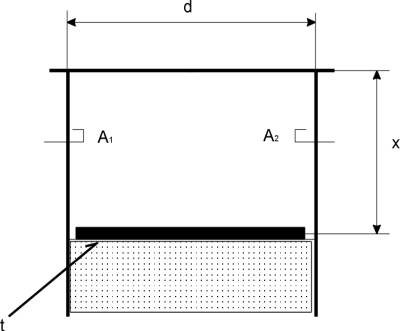
2.  Zasada pomiaru poziomu cieczy za pomocą mikrofalowego rezonatora cylindrycznego

Falowód wnękowy stanowi rezonansowy obwód RLC o stałych rozłożonych. Przemieszczanie jednej ze ścian falowodu wnękowego prowadzi do jednoczesnej zmiany pojemności i indukcyjności układu zastępczego rezonatora. Rozważany czujnik położenia stanowi cylindryczny rezonator mikrofalowy o ruchomej podstawie. Rezonator cylindryczny jest odcinkiem falowodu o przekroju kołowym o średnicy  d  i długości x, którego oba końce zwarto. W rezonatorze tego typu może być wzbudzonych wiele typów drgań rezonansowych, zarówno rodzaju magnetycznego TMmnp  jak i rodzaju elektrycznego TEmnp  [1 - 4]. Z punktu widzenia zastosowań rezonatora do pomiaru przemieszczeń najbardziej przydatny jest rodzaj drgań TE­011, dla którego zwieracze rezonatora mogą stanowić płaskie okrągłe denka przewodzące o średnicy mniejszej niż średnica wewnętrzna falowodu. W przypadku pomiaru poziomu cieczy ruchomą ścianą rezonatora może stanowić metalizowany jednostronnie pływak wykonany z materiału zapewniającego mniejszą zwilżalność cieczą niż wewnętrzne ścianki rezonatora, co zapewnia współosiowy ruch pływaka bez udziału tarcia statycznego (rys. 1).

        Rodzaj drgań TE011 cechuje się dużą szerokopasmowością przestrajania bez obawy wzbudzania innych rodzajów drgań, zapewniając duży zakres pomiarowy czujnika. O właściwościach rezonatora decyduje parametr geometryczny p = d /x.

 Pomiędzy częstotliwością rezonansową rezonatora fr  a parametrem p spełniony  jest związek

                                                                    fr = c1  + c2 p2                                                     (1)

gdzie c1   i c2    są stałymi związanymi z geometrią pola elektromagnetycznego rodzaju TE011.

Rys.1. Mikrofalowy rezonator cylindryczny jako czujnik poziomu cieczy;

t - ruchomy tłok - pływak, A1, A2  - antenki pomiarowe.

Pomiar częstotliwości rezonansowej rezonatora czujnika może być prowadzony metodą odbiciową lub transmisyjną. Zakres przestrajania rezonatora jest ograniczony ryzykiem wystąpienia innych rodzajów drgań, a także właściwościami fizycznymi rodzaju TE011. Jeżeli parametr  p   zmienia się w granicach  pΠ <p1, p2>  wówczas zakres przestrajania

 

                                                                                                                                               (2)

Rodzaj TE011 występuje jako wyłączony w zakresie  p1 = 1,38  do  p2 = 1,76. Odpowiadający mu zakres pomiarowy wynosi

                                                                                                                          (3)

Maksymalne przestrojenie rezonatora odpowiadające rodzajowi  TE011  jest odpowiednio większe i może się odbyć w zakresie

                                                                                                                         (4)

Czynnikiem sprzyjającym zapobieganiu powstawania innych rodzajów drgań, poza TE011, jest brak kontaktu elektrycznego pomiędzy tłokiem rezonatora a jego ścianą boczną.

3.   Zasada pomiaru poziomu cieczy przy użyciu ćwierćfalowego rezonatora współosiowego

Podstawę metody stanowi ćwierćfalowy rezonator współosiowy przestrajany poprzez zmianę poziomu wypełniającej go cieczy dielektrycznej (rys. 2). Przestrajanie rezonatora spowodowane jest zmianą prędkości rozchodzenia się pola elektromagnetycznego w tej jego części, która wypełnia ciecz dielektryczna. Pole elektromagnetyczne typu TEM w rezonatorze współosiowym  jest opisane przez takie samo rozwiązanie jakie uzyskuje się dla fali stojącej w linii współosiowej [3, 4]. W rezonatorze będącym w stanie rezonansu znajduje się fragment tego rozwiązania (względem zmiennej x), warunki rezonansu i sposób wykonania rezonatora wymagają by na zwartym końcu rezonatora wystąpił węzeł fali, na końcu otwartym zaś strzałka. Jeżeli l jest długością rezonatora oznacza to, że musi być spełniony warunek

                                                      ,                                                       (5)

gdzie l r  jest długością fali elektromagnetycznej w stanie rezonansu a n = 0, 1, 2,.. Rezonans ćwierćfalowy stanowi przypadek najprostszy, gdy  n=0.

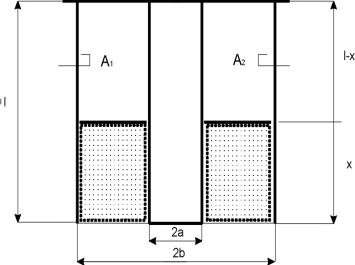
Rys.2. Wnęka ćwierćfalowa jako czujnik poziomu cieczy; A1, A2 - antenki pomiarowe

Wyznaczenie częstotliwości rezonansowej rezonatora nie jest trudne gdy zauważymy, że pomiędzy częstotliwością rezonansową fali  fr  a długością fali lr zachodzi związek

                                                                                                                                 (6)

Podstawiając powyższą formułę do (5)  dla n=0 uzyskamy

                                                                                                                              (7)

Wyrażenie to można zapisać w bardziej wygodnej do dalszych rozważań postaci

                                                                                                                              (8)

gdzie  t = l / v  jest czasem przejścia fali elektromagnetycznej przez rezonator. Gdy rezonator o długości  l  jest częściowo zanurzony w cieczy dielektrycznej o względnej przenikalności dielektrycznej e  na głębokości x  (rys.2), całkowity czas propagacji fali wewnątrz niego będzie sumą czasów propagacji

                                                                                                                    (9)

gdzie  te = x / ve jest czasem przejścia fali przez dielektryk a to = (1-x) / vo czasem przejścia fali przez pustą część rezonatora. Ponieważ prędkości propagacji pola elektromagnetycznego są odpowiednio równe

                                                                 i                                         (10)

gdzie c jest prędkością fali w próżni, formuła (8)  po podstawieniu (10)  i (9) przyjmie postać

                                                                                                           (11)

Uzyskana formuła jest przybliżona, gdyż przyjęte powyżej założenia (9) i (10) są równoznaczne przyjęciu przybliżenia optyki geometrycznej, tzn. przyjęciu, że lr <<1 oraz
lr <<x co wobec warunku (5), dla n = 0, dalekie jest od prawdy. Poprawną formułę można uzyskać rozwiązując równania Maxwella opisujące pole elektromagnetyczne w rezonatorze, uzyskany wynik jest znacznie bardziej skomplikowany i nie da się zapisać przy użyciu funkcji elementarnych.

        Układ czujnika z rezonatorem ćwierćfalowym nie zawiera żadnych ruchomych elementów mechanicznych. Jego droga pomiarowa nie zależy od średnicy rezonatora a jedynie od jego długości, przy czym technicznie możliwe jest osiągnięcie drogi pomiarowej

                                                                                                                              (12)

Średnica rezonatora ma wpływ na jego dobroć elektryczną, parametr ten jak wykażemy poniżej wiąże się ze zdolnością rozdzielczą czujnika.

3.1.  Zdolność rozdzielcza i dokładność czujnika

        O zdolności rozdzielczej dx i dokładności pomiaru położenia dx czujnika decydują rozdzielczość i powtarzalność pomiaru jego częstotliwości rezonansowej. Gdy charakterystyka przestrajania jest dana przez funkcję

                                                                                                                             (13)

wówczas

                                                                                                                  (14)

lub

                                                                                                                    (15)

gdzie

                                                                                                                           (16)

jest czułością charakterystyki przestrajania czujnika w punkcie pomiarowym x . O zdolności rozdzielczej dx czujnika decyduje zatem czułość charakterystyki przestrajania czujnika względem x i zdolność rozdzielcza dfr układu wyznaczającego częstotliwość rezonansową czujnika. O wartości dfr decyduje budowa układu elektronicznego dokonującego pomiaru częstotliwości rezonansowej czujnika. Układy wyznaczające fr  czujnika dokonują analizy krzywej rezonansowej czujnika (rys.3).


 

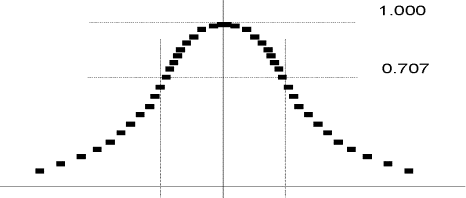
Rys.3. Lorentzowska krzywa rezonansowa przetwornika radiotechnicznego.

Krzywa ta ma szerokość  2Df  zależną od dobroci Q czujnika

                                                                                                                              (17)

Zadaniem układu jest znalezienie częstotliwości odpowiadającej wierzchołkowi krzywej. Układ realizuje to zazwyczaj ze zdolnością rozdzielczą dfr  znacznie przewyższającą szerokość 2Df , co można zapisać w postaci zależności

                                                     ,                                                            (18)

przy czym o jakości pomiaru decyduje współczynnik a <<1. Typowa techniczna wartość tego współczynnika to a = 10-3. Wstawiając (17) do (18) a wynik do (15)  otrzymamy

                                                                                                                           (19)

Uzyskanie dużej zdolności rozdzielczej wymaga dużej dobroci rezonatora i wysokiej czułości charakterystyki przestrajania. Często stosowaną miarą możliwości pomiarowych czujników jest względna zdolność rozdzielcza

                                                                    ,                                                                 (20)

gdzie Dx = xmax - xmin jest zakresem pomiarowym czujnika. Odwrotność wyrażenia (20) określa maksymalną liczbę punktów pomiarowych, którą rozróżnia czujnik na całej drodze pomiarowej.

Przykład :

Czujnik jest rezonatorem ćwierćfalowym o krzywej przestrajania (11)

                                                                                                                      

gdzie e =-1 , stąd

                          

i

                                                                   

Po podstawieniu do (19) otrzymamy

           

Dla czujnika MCL 50 o parametrach roboczych:

 

l = 250 mm

Dx = 0,2 l = 50 mm

x = 0,15 l, położenie cieczy dielektrycznej odpowiadające „0” czujnika

e = 2,69, stała oleju silnikowego OM 20

e= 0,64

Q =1400  (dobroć techniczna rezonatora)

fmax = 305 MHz

fmin  = 245 MHz

a = 0,001 (typowa wartość)

uzyskuje się zdolności rozdzielcze:

dx ť 0,3 mm.

dx/Dx ť 6 ×10­-6.

Podobnie dla czujnika MCL 500 o parametrach:

l = 1500 mm

Dx = 0,33 l = 500 mm

x = 0,20 l ,poziom "0" czujnika

e = 2,69

e = 0,64

Q = 800

a = 0,001

fmax = 52 MHz

fmin = 34 MHz

uzyskuje się:

dx = 3 um.

dx / Dx = 6 ×10-6

Oznacza to, że obydwa czujniki rozróżniają około Dx / dx ť 150 000 punktów pomiarowych w całym zakresie pomiarowym.

        Dokładność czujnika jest tym większa im mniejsza jest czułość jego charakterystyki przestrajania na zewnętrzne czynniki zakłócające. Przy stabilnej konstrukcji mechanicznej czujnika, praktycznie jedynym czynnikiem zmieniającym jego parametry jest zmiana temperatury . Zmiana temperatury prowadzi do zmiany długości czujnika, oraz do zmiany gęstości i stałej dielektrycznej cieczy. W praktyce zależność stałej dielektrycznej cieczy od temperatury (dla oleju silikonowego OM 20 de¤e ť 1,5*10-3 1/°C ) ma największy wpływ na pracę czujnika. W czujniku MCL 50 zmiana temperatury o 1°C prowadzi do zmiany |dx|@10um . Aby ten wpływ wyeliminować czujniki wyposaża się w termometry platynowe. Pomiar temperatury pozwala na uwzględnienie poprawek temperaturowych i osiągnięcie w szerokim zakresie temperatur dokładności

Zdolność czujnika do długoczasowego przechowania charakterystyki jest bardzo dobra. Charakterystyka ta zależna jest wyłącznie od wymiarów geometrycznych rezonatora, które mogą pozostać niezmienione w długim przedziale czasu.

3.2. Elektroniczny pomiar częstotliwości rezonansowej czujnika

Częstotliwości rezonansowe czujników radiotechnicznych można wyznaczyć dwiema metodami.

Metoda I

        Układ rezonansowy przetwornika odtłumia się poprzez wtrącenie ujemnej oporności rzeczywistej do obwodu (r< 0) tak aby spełniony był warunek generacji, tzn. r+R £ 0 (rys.4). Częstotliwość własna oscylacji powstających w obwodzie jest mierzona cyfrowym miernikiem częstotliwości włączonym w sposób niezaburzający pracy obwodu.

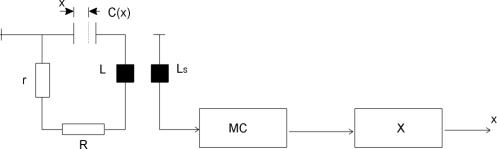
Rys.4. Metoda I pomiaru częstotliwości rezonansowej przetwornika; Ls - układ sprzęgający,

MC - miernik częstotliwości, X - przetwornik częstotliwość- położenie.

Częstotliwość fr, a także wartość mierzonej jednocześnie temperatury T, stanowią podstawę do numerycznego obliczenia położenia x przy znajomości charakterystyki przetwornika
x = g(fr, T). Metoda generacyjna zapewnia uzyskanie współczynnika a @ 0.001.

Metoda II

W tej metodzie rezonator jest sprzężony transmisyjnie z aparaturą pomiarową przy pomocy linii przesyłowych. Układ sterujący US aparatury pomiarowej (rys.5) wytwarza narastający liniowo przebieg piłokształtny przestrajający napięciowo generator GPN. Gdy częstotliwość generatora fg zbliży się dostatecznie do częstotliwości rezonansowej przetwornika fr, staje się możliwa transmisja sygnału poprzez rezonator czujnika do układu detekcyjnego D. Przekroczenie ustalonego progu przez sygnał detekcyjny unieruchamia narastanie przebiegu piłokształtnego i włącza układ szukania wierzchołka krzywej rezonansu USW. Układ USW szuka takiego napięcia zasilającego GPN, przy którym transmisja sygnału przez czujnik jest maksymalna. Odpowiada to warunkowi fg  =  fr.

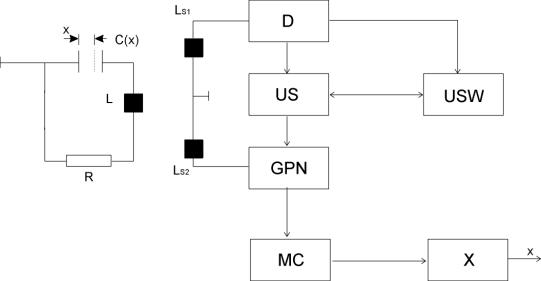
Rys.5. Metoda II transmisyjnego pomiaru częstotliwości rezonansowej przetwornika radiotechnicznego; Ls1 - odbiorczy układ sprzęgający, Ls2 - nadawczy układ sprzęgający, D - detektor, U S - układ sterujący, G P N - generator przestrajany napięciowo, U S W - układ szukania wierzchołka, M C - miernik częstotliwości, X - przetwornik częstotliwość-położenie.

W metodzie tej należy zwrócić uwagę na ewentualny wpływ nieskompensowanych reakcji  linii zasilających na częstotliwość rezonansową czujnika. Problem ten związany jest z trudnością zapewnienia małostratnego dopasowania czujnika do lini transmisyjnej w całym zakresie częstotliwości jego pracy. Gdy nieskompensowane reakcje na wejściu i wyjściu rezonatora są równe x1 i x2, a współczynniki sprzężenia z linią odpowiednio s1 i s2, wówczas względne przestrojenie rezonatora jest równe

                                                     ,                                                 (21)

gdzie Z0 jest opornością falową linii. Gdy zażąda się by rozstrojenie (21) było nie większe niż względne mierzalne przestrojenie opisane formułą (18), wówczas dla s1 = s2 = 0,5 i x1 = x2 = x uzyskuje się wartość numeryczną względnego niedopasowania równą X/Z0 £ 0,2. W praktyce można ten warunek osłabić przyjmując mniejsze wartości współczynników sprzężenia s1  i s2.

Częstotliwość fg generatora GPN odpowiadająca wierzchołkowi krzywej rezonansu jest mierzona i wraz z wynikiem pomiaru temperatury służy do obliczenia położenia poziomu cieczy x jak poprzednio. Podobnie jak w metodzie I, typową uzyskiwaną wartością współczynnika a  jest 0,001.

4. Zadania do wykonania.

  1. Przećwiczyć odczyt wskazania katetometru i sterowanie przepływem cieczy.
  2. Zmieniając poziom cieczy wypełniającej rezonator od poziomu 50cm do 20cm z krokiem 1cm obserwować i notować zmiany częstotliwości rezonansowej oraz rezystancji rezystora platynowego Pt1000, działającego jako czujnik temperatury. Odczytu częstotliwości należy dokonywać po ustabilizowaniu się poziomu cieczy.
  3. Korzystając z zależności rezystancji od temperatury dla Pt1000 obliczyć minimalną, maksymalną oraz średnią temperaturę, jaką miała ciecz podczas pomiarów.
  4. Korzystając z zebranych danych wykreślić zależność x(fr) - poziomu cieczy w rezonatorze w funkcji częstotliwości rezonansowej. Wyjaśnić kształt powstałego wykresu.
  5. Wyznaczyć funkcję kwadratową (odcinek paraboli), która może aproksymować krzywą x(fr). Korzystając z tej aproksymacji obliczyć zdolność rozdzielczą czujnika:

    wzor_spr1   [mm], 

    gdzie df [Hz] jest dokładnością pomiaru częstotliwości rezonansowej (można założyć że jest to dokładność wskazania dołączonego do zestawu częstotliwościomierza).

    Zdolność rozdzielczą przedstawia się często również w postaci unormowanej - logarytmicznej:

    wzor_spr2  [dB]

    gdzie Dx = xmax - xmin  jest drogą pomiarową.

    Obliczyć zdolność rozdzielczą w [mm] i [dB] dla 3 poziomów cieczy: najmniejszego, największego i w połowie zakresu pomiarów. Jak zmienia się ta zdolność wraz ze zmianami poziomu cieczy?

  6. Na bezwzględny błąd odczytu poziomu cieczy w badanym układzie pomiarowym ma wpływ kilka składników. Są to np. błędy odczytu urządzeń pomiarowych podczas wyznaczania charakterystyk czujnika. Spróbować wymienić pozostałe źródła błędów oraz przedyskutować ich ewentualny wpływ na pomiar.

5. Literatura

1.      R.P  Feynman R. B. Leighton M. Sands, Feynmama wykłady z fizyki, tom II, część 2, rozdz. 23, 24, PWN, Warszawa 1970 i kolejne wydania.

2.      D. Halliday R.Resnick , Fizyka dla studentów nauk przyrodniczych i technicznych, tom II rozdz. 38, 39, PWN, Warszawa 1974 i kolejne wydania.

3.      E. L. Ginzton, Microwave Measurements, Mc. Graw. Hill 1957.

4.      R. E. Collin, Prowadzenie fal elektromagnetycznych, WNT, Warszawa 1966.

5.      R. Litwin, M. Suski, Technika mikrofalowa, WNT, Warszawa 1972.

6.      B. Galwas, Miernictwo mikrofalowe, WKŁ, Warszawa 1985.